ધ્રુવીકરણ એ એન્ટેનાની મૂળભૂત લાક્ષણિકતાઓમાંની એક છે. આપણે પહેલા સમતલ તરંગોના ધ્રુવીકરણને સમજવાની જરૂર છે. ત્યારબાદ આપણે એન્ટેના ધ્રુવીકરણના મુખ્ય પ્રકારોની ચર્ચા કરી શકીએ છીએ.
રેખીય ધ્રુવીકરણ
આપણે સમતલ ઇલેક્ટ્રોમેગ્નેટિક તરંગના ધ્રુવીકરણને સમજવાનું શરૂ કરીશું.
પ્લેનર ઇલેક્ટ્રોમેગ્નેટિક (EM) તરંગમાં ઘણી લાક્ષણિકતાઓ હોય છે. પહેલું એ છે કે પાવર એક દિશામાં પ્રવાસ કરે છે (બે ઓર્થોગોનલ દિશામાં કોઈ ક્ષેત્ર બદલાતું નથી). બીજું, ઇલેક્ટ્રિક ક્ષેત્ર અને ચુંબકીય ક્ષેત્ર એકબીજાને લંબ અને ઓર્થોગોનલ છે. ઇલેક્ટ્રિક અને ચુંબકીય ક્ષેત્રો પ્લેન તરંગ પ્રસારની દિશામાં લંબ છે. ઉદાહરણ તરીકે, સમીકરણ (1) દ્વારા આપવામાં આવેલ એકલ-આવર્તન ઇલેક્ટ્રિક ક્ષેત્ર (E ક્ષેત્ર) ને ધ્યાનમાં લો. ઇલેક્ટ્રોમેગ્નેટિક ક્ષેત્ર +z દિશામાં પ્રવાસ કરી રહ્યું છે. ઇલેક્ટ્રિક ક્ષેત્ર +x દિશામાં નિર્દેશિત છે. ચુંબકીય ક્ષેત્ર +y દિશામાં છે.
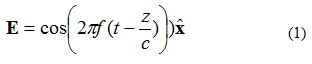
સમીકરણ (1) માં, સંકેતનું અવલોકન કરો: . આ એક એકમ વેક્ટર (લંબાઈનો વેક્ટર) છે, જે કહે છે કે ઇલેક્ટ્રિક ક્ષેત્ર બિંદુ x દિશામાં છે. સમતલ તરંગ આકૃતિ 1 માં દર્શાવવામાં આવ્યું છે.
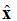
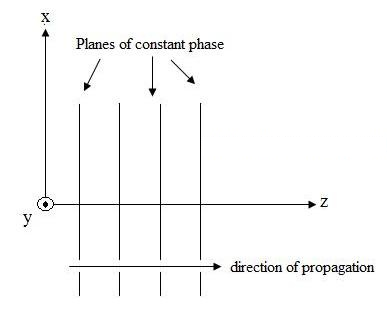
આકૃતિ 1. +z દિશામાં ગતિ કરતા વિદ્યુત ક્ષેત્રનું ગ્રાફિકલ પ્રતિનિધિત્વ.
ધ્રુવીકરણ એ વિદ્યુત ક્ષેત્રનો ટ્રેસ અને પ્રચાર આકાર (કોન્ટૂર) છે. ઉદાહરણ તરીકે, પ્લેન વેવ વિદ્યુત ક્ષેત્ર સમીકરણ (1) ને ધ્યાનમાં લો. આપણે સમયના કાર્ય તરીકે વિદ્યુત ક્ષેત્ર (X,Y,Z) = (0,0,0) છે તે સ્થિતિનું અવલોકન કરીશું. આ ક્ષેત્રનું કંપનવિસ્તાર આકૃતિ 2 માં, સમયમાં અનેક વખત દર્શાવવામાં આવ્યું છે. ક્ષેત્ર "F" આવૃત્તિ પર ઓસીલેટીંગ કરી રહ્યું છે.
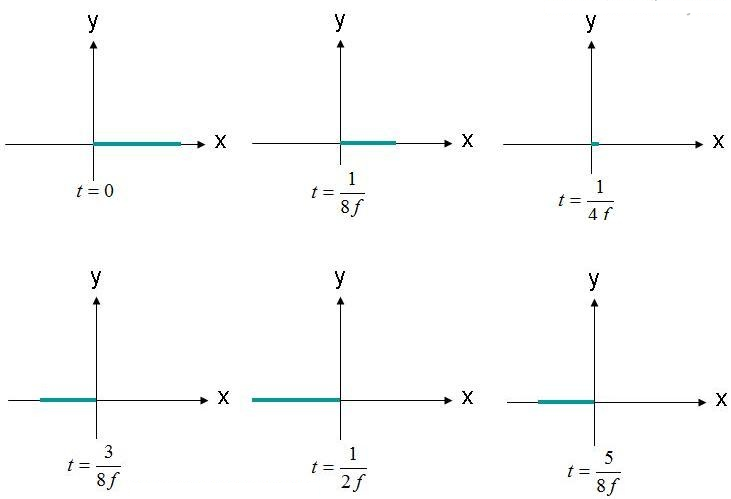
આકૃતિ 2. જુદા જુદા સમયે વિદ્યુત ક્ષેત્ર (X, Y, Z) = (0,0,0) નું અવલોકન કરો.
વિદ્યુત ક્ષેત્ર મૂળ સ્થાને જોવા મળે છે, જે કંપનવિસ્તારમાં આગળ પાછળ ફરતું હોય છે. વિદ્યુત ક્ષેત્ર હંમેશા દર્શાવેલ x-અક્ષ સાથે હોય છે. કારણ કે વિદ્યુત ક્ષેત્ર એક જ રેખા સાથે જાળવવામાં આવે છે, આ ક્ષેત્રને રેખીય રીતે ધ્રુવીકરણ થયેલ કહી શકાય. વધુમાં, જો X-અક્ષ જમીનની સમાંતર હોય, તો આ ક્ષેત્રને આડી રીતે ધ્રુવીકરણ થયેલ તરીકે પણ વર્ણવવામાં આવે છે. જો ક્ષેત્ર Y-અક્ષ સાથે દિશામાન હોય, તો તરંગ ઊભી રીતે ધ્રુવીકરણ થયેલ કહી શકાય.
રેખીય રીતે ધ્રુવીકરણ કરાયેલા તરંગોને આડી અથવા ઊભી ધરી સાથે દિશામાન કરવાની જરૂર નથી. ઉદાહરણ તરીકે, આકૃતિ 3 માં બતાવ્યા પ્રમાણે રેખા સાથે અવરોધ ધરાવતી ઇલેક્ટ્રિક ક્ષેત્ર તરંગ પણ રેખીય રીતે ધ્રુવીકરણવાળી હશે.
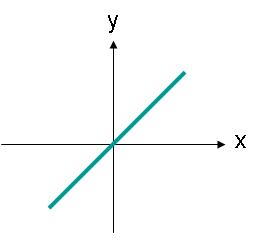
છબી 3. રેખીય ધ્રુવીકૃત તરંગનું વિદ્યુત ક્ષેત્ર કંપનવિસ્તાર જેનો માર્ગ એક ખૂણો છે.
આકૃતિ 3 માં દર્શાવેલ વિદ્યુત ક્ષેત્રનું વર્ણન સમીકરણ (2) દ્વારા કરી શકાય છે. હવે વિદ્યુત ક્ષેત્રનો x અને y ઘટક છે. બંને ઘટકો કદમાં સમાન છે.
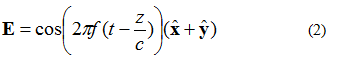
સમીકરણ (2) વિશે એક વાત નોંધનીય છે કે બીજા તબક્કામાં xy-ઘટક અને ઇલેક્ટ્રોનિક ક્ષેત્રો છે. આનો અર્થ એ છે કે બંને ઘટકો હંમેશા સમાન કંપનવિસ્તાર ધરાવે છે.
ગોળાકાર ધ્રુવીકરણ
હવે ધારો કે સમતલ તરંગનું વિદ્યુત ક્ષેત્ર સમીકરણ (3) દ્વારા આપવામાં આવ્યું છે:
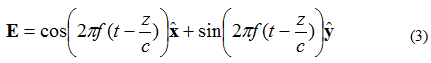
આ કિસ્સામાં, X- અને Y-તત્વો તબક્કાની બહાર 90 ડિગ્રી છે. જો ક્ષેત્રને પહેલાની જેમ ફરીથી (X, Y, Z) = (0,0,0) તરીકે અવલોકન કરવામાં આવે, તો વિદ્યુત ક્ષેત્ર વિરુદ્ધ સમય વળાંક આકૃતિ 4 માં નીચે બતાવ્યા પ્રમાણે દેખાશે.
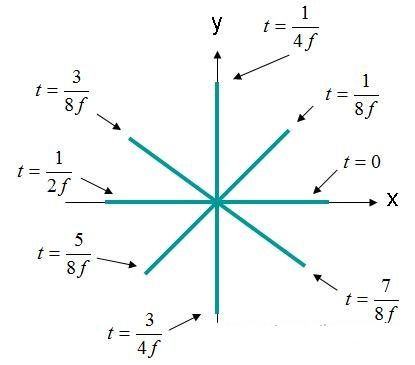
આકૃતિ 4. વિદ્યુત ક્ષેત્ર શક્તિ (X, Y, Z) = (0,0,0) EQ ડોમેન. (3).
આકૃતિ 4 માં દર્શાવેલ વિદ્યુત ક્ષેત્ર વર્તુળમાં ફરે છે. આ પ્રકારના ક્ષેત્રને ગોળાકાર ધ્રુવીકરણ તરંગ તરીકે વર્ણવવામાં આવ્યું છે. ગોળાકાર ધ્રુવીકરણ માટે, નીચેના માપદંડો પૂર્ણ કરવા આવશ્યક છે:
- ગોળાકાર ધ્રુવીકરણ માટે માનક
- વિદ્યુત ક્ષેત્રમાં બે ઓર્થોગોનલ (લંબ) ઘટકો હોવા જોઈએ.
- ઇલેક્ટ્રિક ક્ષેત્રના ઓર્થોગોનલ ઘટકોમાં સમાન કંપનવિસ્તાર હોવા જોઈએ.
- ચતુર્ભુજ ઘટકો તબક્કાની બહાર 90 ડિગ્રી હોવા જોઈએ.
જો વેવ આકૃતિ 4 સ્ક્રીન પર મુસાફરી કરી રહ્યા હોય, તો ક્ષેત્ર પરિભ્રમણ ઘડિયાળની વિરુદ્ધ દિશામાં અને જમણા હાથે ગોળાકાર ધ્રુવીકરણ (RHCP) કહેવાય છે. જો ક્ષેત્ર ઘડિયાળની દિશામાં ફેરવવામાં આવે, તો ક્ષેત્ર ડાબા હાથે ગોળાકાર ધ્રુવીકરણ (LHCP) હશે.
લંબગોળ ધ્રુવીકરણ
જો વિદ્યુત ક્ષેત્રમાં બે લંબ ઘટકો હોય, તબક્કાની બહાર 90 ડિગ્રી પરંતુ સમાન તીવ્રતા હોય, તો ક્ષેત્ર લંબગોળ ધ્રુવીકરણ પામશે. સમીકરણ (4) દ્વારા વર્ણવેલ +z દિશામાં ગતિ કરતી સમતલ તરંગના વિદ્યુત ક્ષેત્રને ધ્યાનમાં લેતા:
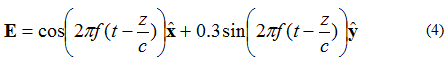
ઇલેક્ટ્રિક ફિલ્ડ વેક્ટરનો છેડો જે બિંદુ પર ધારણ કરશે તેનું સ્થાન આકૃતિ 5 માં આપેલ છે.
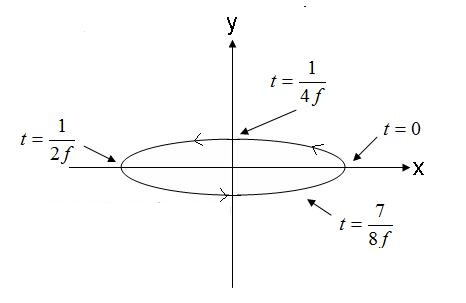
આકૃતિ 5. લંબગોળ ધ્રુવીકરણ તરંગ વિદ્યુત ક્ષેત્રને પ્રોમ્પ્ટ કરો. (4).
આકૃતિ 5 માં દર્શાવેલ ક્ષેત્ર, ઘડિયાળની વિરુદ્ધ દિશામાં ગતિ કરે છે, જો તે સ્ક્રીનની બહાર ફરે તો જમણા હાથે લંબગોળ હશે. જો ઇલેક્ટ્રિક ક્ષેત્ર વેક્ટર વિરુદ્ધ દિશામાં ફરે છે, તો ક્ષેત્ર ડાબા હાથે લંબગોળ ધ્રુવીકરણ પામશે.
વધુમાં, લંબગોળ ધ્રુવીકરણ તેની વિષમતાનો ઉલ્લેખ કરે છે. મુખ્ય અને ગૌણ અક્ષોના કંપનવિસ્તાર સાથે વિષમતાનો ગુણોત્તર. ઉદાહરણ તરીકે, સમીકરણ (4) માંથી તરંગ વિષમતા 1/0.3= 3.33 છે. લંબગોળ ધ્રુવીકરણ તરંગોને મુખ્ય અક્ષની દિશા દ્વારા વધુ વર્ણવવામાં આવે છે. તરંગ સમીકરણ (4) માં મુખ્યત્વે x-અક્ષનો સમાવેશ થતો અક્ષ છે. નોંધ કરો કે મુખ્ય અક્ષ કોઈપણ સમતલ ખૂણા પર હોઈ શકે છે. કોણ X, Y અથવા Z અક્ષને ફિટ કરવા માટે જરૂરી નથી. છેલ્લે, એ નોંધવું મહત્વપૂર્ણ છે કે ગોળાકાર અને રેખીય ધ્રુવીકરણ બંને લંબગોળ ધ્રુવીકરણના ખાસ કિસ્સાઓ છે. 1.0 તરંગી લંબગોળ ધ્રુવીકરણ તરંગ એક ગોળાકાર ધ્રુવીકરણ તરંગ છે. અનંત વિષમતા સાથે લંબગોળ ધ્રુવીકરણ તરંગો. રેખીય ધ્રુવીકરણ તરંગો.
એન્ટેના ધ્રુવીકરણ
હવે જ્યારે આપણે ધ્રુવીકૃત પ્લેન વેવ ઇલેક્ટ્રોમેગ્નેટિક ક્ષેત્રોથી વાકેફ છીએ, તો એન્ટેનાનું ધ્રુવીકરણ સરળ રીતે વ્યાખ્યાયિત કરવામાં આવ્યું છે.
એન્ટેના ધ્રુવીકરણ એક એન્ટેના દૂર-ક્ષેત્ર મૂલ્યાંકન, પરિણામી રેડિયેટેડ ક્ષેત્રનું ધ્રુવીકરણ. તેથી, એન્ટેનાને ઘણીવાર "રેખીય ધ્રુવીકરણ" અથવા "જમણા હાથના ગોળાકાર ધ્રુવીકરણવાળા એન્ટેના" તરીકે સૂચિબદ્ધ કરવામાં આવે છે.
આ સરળ ખ્યાલ એન્ટેના સંદેશાવ્યવહાર માટે મહત્વપૂર્ણ છે. પ્રથમ, આડી ધ્રુવીકરણ કરેલ એન્ટેના ઊભી ધ્રુવીકરણ કરેલ એન્ટેના સાથે વાતચીત કરશે નહીં. પારસ્પરિકતા પ્રમેયને કારણે, એન્ટેના બરાબર એ જ રીતે પ્રસારિત થાય છે અને પ્રાપ્ત કરે છે. તેથી, ઊભી ધ્રુવીકરણ કરેલ એન્ટેના ઊભી ધ્રુવીકરણ કરેલ ક્ષેત્રોને પ્રસારિત કરે છે અને પ્રાપ્ત કરે છે. તેથી, જો તમે ઊભી ધ્રુવીકરણ કરેલ આડી ધ્રુવીકરણ કરેલ એન્ટેનાને પહોંચાડવાનો પ્રયાસ કરો છો, તો કોઈ સ્વાગત થશે નહીં.
સામાન્ય કિસ્સામાં, બે રેખીય ધ્રુવીકૃત એન્ટેના માટે જે એકબીજાની સાપેક્ષમાં એક ખૂણા ( ) દ્વારા ફેરવાય છે, આ ધ્રુવીકરણ મિસમેચને કારણે પાવર લોસનું વર્ણન ધ્રુવીકરણ નુકશાન પરિબળ (PLF) દ્વારા કરવામાં આવશે:
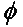
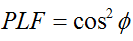
તેથી, જો બે એન્ટેનામાં સમાન ધ્રુવીકરણ હોય, તો તેમના રેડિયેટિંગ ઇલેક્ટ્રોન ક્ષેત્રો વચ્ચેનો ખૂણો શૂન્ય હોય છે અને ધ્રુવીકરણ મેળ ખાતી ન હોવાથી પાવર લોસ થતો નથી. જો એક એન્ટેના ઊભી ધ્રુવીકરણવાળી હોય અને બીજી આડી ધ્રુવીકરણવાળી હોય, તો કોણ 90 ડિગ્રી હોય છે, અને કોઈ પાવર ટ્રાન્સફર થશે નહીં.
નોંધ: ફોનને તમારા માથા ઉપર અલગ અલગ ખૂણા પર ખસેડવાથી સમજાવે છે કે ક્યારેક રિસેપ્શન કેમ વધારી શકાય છે. સેલ ફોન એન્ટેના સામાન્ય રીતે રેખીય રીતે ધ્રુવીકરણ પામેલા હોય છે, તેથી ફોનને ફેરવવાથી ઘણીવાર ફોનના ધ્રુવીકરણ સાથે મેળ ખાય છે, આમ રિસેપ્શનમાં સુધારો થાય છે.
ગોળાકાર ધ્રુવીકરણ એ ઘણા એન્ટેનાની ઇચ્છનીય લાક્ષણિકતા છે. બંને એન્ટેના ગોળાકાર ધ્રુવીકરણવાળા હોય છે અને ધ્રુવીકરણના મેળ ખાતી ન હોવાથી સિગ્નલ નુકશાનનો ભોગ બનતા નથી. GPS સિસ્ટમમાં વપરાતા એન્ટેના જમણી બાજુ ગોળાકાર ધ્રુવીકરણવાળા હોય છે.
હવે ધારો કે એક રેખીય ધ્રુવીકરણ એન્ટેના ગોળાકાર ધ્રુવીકરણ તરંગો પ્રાપ્ત કરે છે. સમાન રીતે, ધારો કે એક ગોળાકાર ધ્રુવીકરણ એન્ટેના રેખીય ધ્રુવીકરણ તરંગો પ્રાપ્ત કરવાનો પ્રયાસ કરે છે. પરિણામી ધ્રુવીકરણ નુકશાન પરિબળ શું છે?
યાદ કરો કે ગોળાકાર ધ્રુવીકરણ વાસ્તવમાં બે ઓર્થોગોનલ રેખીય ધ્રુવીકરણ તરંગો છે, જે તબક્કાની બહાર 90 ડિગ્રી છે. તેથી, રેખીય ધ્રુવીકરણ (LP) એન્ટેના ફક્ત ગોળાકાર ધ્રુવીકરણ (CP) તરંગ તબક્કા ઘટક પ્રાપ્ત કરશે. તેથી, LP એન્ટેનામાં 0.5 (-3dB) નું ધ્રુવીકરણ મિસમેચ નુકશાન હશે. LP એન્ટેના ગમે તે ખૂણા પર ફેરવવામાં આવે તો પણ આ સાચું છે. તેથી:
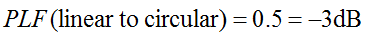
ધ્રુવીકરણ નુકશાન પરિબળને ક્યારેક ધ્રુવીકરણ કાર્યક્ષમતા, એન્ટેના મિસમેચ ફેક્ટર અથવા એન્ટેના રિસેપ્શન ફેક્ટર તરીકે ઓળખવામાં આવે છે. આ બધા નામો સમાન ખ્યાલનો સંદર્ભ આપે છે.
પોસ્ટ સમય: ડિસેમ્બર-22-2023







