જ્યારે વાત આવે છેએન્ટેના, લોકો જે પ્રશ્ન વિશે સૌથી વધુ ચિંતિત છે તે છે "કિરણોત્સર્ગ ખરેખર કેવી રીતે પ્રાપ્ત થાય છે?" સિગ્નલ સ્ત્રોત દ્વારા ઉત્પન્ન થયેલ ઇલેક્ટ્રોમેગ્નેટિક ક્ષેત્ર ટ્રાન્સમિશન લાઇન દ્વારા અને એન્ટેનાની અંદર કેવી રીતે પ્રસારિત થાય છે, અને અંતે એન્ટેનાથી "અલગ" થઈને મુક્ત અવકાશ તરંગ બનાવે છે.
૧. સિંગલ વાયર રેડિયેશન
ચાલો ધારીએ કે ચાર્જ ઘનતા, જે qv (કૌલોમ્બ/m3) તરીકે દર્શાવવામાં આવે છે, તે આકૃતિ 1 માં બતાવ્યા પ્રમાણે, a ના ક્રોસ-સેક્શનલ ક્ષેત્રફળ અને V ના વોલ્યુમવાળા ગોળાકાર વાયરમાં સમાન રીતે વિતરિત થાય છે.
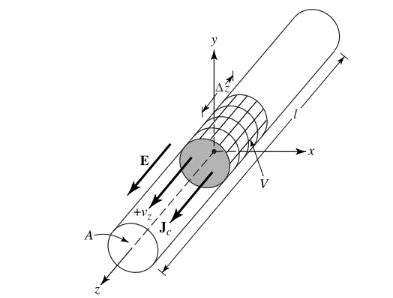
આકૃતિ 1
વોલ્યુમ V માં કુલ ચાર્જ Q એક સમાન ગતિએ z દિશામાં ગતિ કરે છે Vz (m/s). તે સાબિત કરી શકાય છે કે વાયરના ક્રોસ સેક્શન પર વર્તમાન ઘનતા Jz છે:
Jz = qv vz (1)
જો વાયર આદર્શ વાહકથી બનેલો હોય, તો વાયરની સપાટી પર વર્તમાન ઘનતા Js છે:
Js = qs vz (2)
જ્યાં qs એ સપાટીના ચાર્જની ઘનતા છે. જો વાયર ખૂબ જ પાતળો હોય (આદર્શ રીતે, ત્રિજ્યા 0 હોય), તો વાયરમાં પ્રવાહ આ રીતે વ્યક્ત કરી શકાય છે:
Iz = ql vz (3)
જ્યાં ql (કુલંબ/મીટર) એ પ્રતિ યુનિટ લંબાઈનો ચાર્જ છે.
આપણે મુખ્યત્વે પાતળા વાયરો સાથે સંબંધિત છીએ, અને ઉપરોક્ત ત્રણ કિસ્સાઓમાં તારણો લાગુ પડે છે. જો પ્રવાહ સમય-બદલતો હોય, તો સમયના સંદર્ભમાં સૂત્ર (3) નું વ્યુત્પન્ન નીચે મુજબ છે:
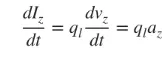
(૪)
az એ ચાર્જ પ્રવેગ છે. જો વાયરની લંબાઈ l હોય, તો (4) નીચે મુજબ લખી શકાય:
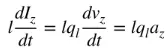
(૫)
સમીકરણ (5) એ વર્તમાન અને ચાર્જ વચ્ચેનો મૂળભૂત સંબંધ છે, અને ઇલેક્ટ્રોમેગ્નેટિક રેડિયેશનનો મૂળભૂત સંબંધ પણ છે. સરળ શબ્દોમાં કહીએ તો, રેડિયેશન ઉત્પન્ન કરવા માટે, સમય-બદલાતો વર્તમાન અથવા ચાર્જનો પ્રવેગ (અથવા ઘટાડો) હોવો આવશ્યક છે. આપણે સામાન્ય રીતે સમય-હાર્મોનિક એપ્લિકેશનોમાં વર્તમાનનો ઉલ્લેખ કરીએ છીએ, અને ચાર્જનો ઉલ્લેખ મોટાભાગે ક્ષણિક એપ્લિકેશનોમાં થાય છે. ચાર્જ પ્રવેગ (અથવા ઘટાડો) ઉત્પન્ન કરવા માટે, વાયર વાળેલો, ફોલ્ડ કરેલ અને અસંતુષ્ટ હોવો જોઈએ. જ્યારે ચાર્જ સમય-હાર્મોનિક ગતિમાં ઓસીલેટ થાય છે, ત્યારે તે સમયાંતરે ચાર્જ પ્રવેગ (અથવા ઘટાડો) અથવા સમય-બદલાતો વર્તમાન પણ ઉત્પન્ન કરશે. તેથી:
૧) જો ચાર્જ ખસેડતો નથી, તો કોઈ પ્રવાહ અને કિરણોત્સર્ગ નહીં હોય.
2) જો ચાર્જ સતત ગતિએ ફરે છે:
a. જો વાયર સીધો અને અનંત લંબાઈનો હોય, તો કોઈ રેડિયેશન થતું નથી.
b. જો આકૃતિ 2 માં બતાવ્યા પ્રમાણે, વાયર વળેલો, ફોલ્ડ થયેલો અથવા અસંબંધિત હોય, તો રેડિયેશન થાય છે.
૩) જો સમય જતાં ચાર્જ ડોલશે, તો વાયર સીધો હોવા છતાં પણ ચાર્જ રેડિયેટ થશે.
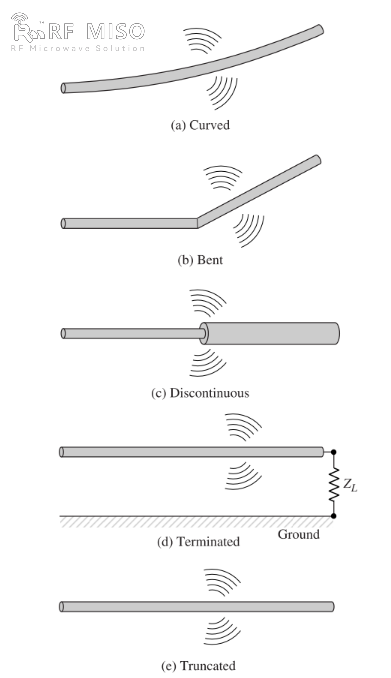
આકૃતિ 2
આકૃતિ 2(d) માં બતાવ્યા પ્રમાણે, ખુલ્લા વાયર સાથે જોડાયેલા સ્પંદિત સ્ત્રોતને જોઈને કિરણોત્સર્ગ મિકેનિઝમની ગુણાત્મક સમજ મેળવી શકાય છે, જે તેના ખુલ્લા છેડા પરના ભાર દ્વારા ગ્રાઉન્ડ થઈ શકે છે. જ્યારે વાયર શરૂઆતમાં ઉર્જાયુક્ત થાય છે, ત્યારે વાયરમાં રહેલા ચાર્જ (મુક્ત ઇલેક્ટ્રોન) સ્ત્રોત દ્વારા ઉત્પન્ન થતી ઇલેક્ટ્રિક ક્ષેત્ર રેખાઓ દ્વારા ગતિમાં સેટ થાય છે. જેમ જેમ વાયરના સ્ત્રોત છેડે ચાર્જ ઝડપી થાય છે અને તેના છેડે પ્રતિબિંબિત થાય છે ત્યારે તે ધીમો પડે છે (મૂળ ગતિની તુલનામાં નકારાત્મક પ્રવેગ), તેના છેડા પર અને બાકીના વાયર સાથે રેડિયેશન ક્ષેત્ર ઉત્પન્ન થાય છે. ચાર્જનું પ્રવેગ બળના બાહ્ય સ્ત્રોત દ્વારા પૂર્ણ થાય છે જે ચાર્જને ગતિમાં સેટ કરે છે અને સંકળાયેલ રેડિયેશન ક્ષેત્ર ઉત્પન્ન કરે છે. વાયરના છેડા પર ચાર્જનું ધીમું થવું પ્રેરિત ક્ષેત્ર સાથે સંકળાયેલા આંતરિક દળો દ્વારા પૂર્ણ થાય છે, જે વાયરના છેડા પર કેન્દ્રિત ચાર્જના સંચયને કારણે થાય છે. આંતરિક દળો ચાર્જના સંચયમાંથી ઊર્જા મેળવે છે કારણ કે તેનો વેગ વાયરના છેડા પર શૂન્ય થઈ જાય છે. તેથી, ઇલેક્ટ્રિક ક્ષેત્ર ઉત્તેજનાને કારણે ચાર્જનું પ્રવેગ અને વાયર ઇમ્પિડન્સના ડિસ્કોન્ટિન્યુટી અથવા સરળ વળાંકને કારણે ચાર્જનું ધીમું થવું એ ઇલેક્ટ્રોમેગ્નેટિક રેડિયેશન ઉત્પન્ન કરવા માટેની પદ્ધતિઓ છે. જોકે મેક્સવેલના સમીકરણોમાં વર્તમાન ઘનતા (Jc) અને ચાર્જ ઘનતા (qv) બંને સ્રોત શબ્દો છે, ચાર્જને વધુ મૂળભૂત જથ્થો માનવામાં આવે છે, ખાસ કરીને ક્ષણિક ક્ષેત્રો માટે. જોકે રેડિયેશનની આ સમજૂતી મુખ્યત્વે ક્ષણિક સ્થિતિઓ માટે વપરાય છે, તેનો ઉપયોગ સ્થિર-સ્થિતિ કિરણોત્સર્ગને સમજાવવા માટે પણ થઈ શકે છે.
ઘણા ઉત્તમ ભલામણ કરોએન્ટેના ઉત્પાદનોદ્વારા ઉત્પાદિતઆરએફએમઆઈએસઓ:
2. બે-વાયર રેડિયેશન
આકૃતિ 3(a) માં બતાવ્યા પ્રમાણે, વોલ્ટેજ સ્ત્રોતને એન્ટેના સાથે જોડાયેલ બે-વાહક ટ્રાન્સમિશન લાઇન સાથે જોડો. બે-વાયર લાઇન પર વોલ્ટેજ લાગુ કરવાથી વાહકો વચ્ચે વિદ્યુત ક્ષેત્ર ઉત્પન્ન થાય છે. વિદ્યુત ક્ષેત્ર રેખાઓ દરેક વાહક સાથે જોડાયેલા મુક્ત ઇલેક્ટ્રોન (પરમાણુઓથી સરળતાથી અલગ) પર કાર્ય કરે છે અને તેમને ખસેડવા માટે દબાણ કરે છે. ચાર્જની ગતિ પ્રવાહ ઉત્પન્ન કરે છે, જે બદલામાં ચુંબકીય ક્ષેત્ર ઉત્પન્ન કરે છે.
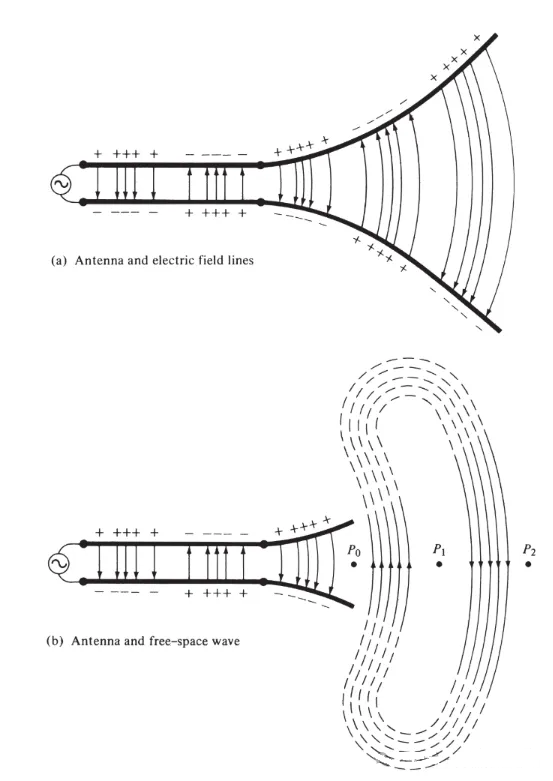
આકૃતિ 3
આપણે સ્વીકાર્યું છે કે ઇલેક્ટ્રિક ફિલ્ડ લાઇન્સ ધન ચાર્જથી શરૂ થાય છે અને ઋણ ચાર્જ સાથે સમાપ્ત થાય છે. અલબત્ત, તેઓ ધન ચાર્જથી શરૂ થઈને અનંત પર પણ સમાપ્ત થઈ શકે છે; અથવા અનંત પર શરૂ થઈને ઋણ ચાર્જ સાથે સમાપ્ત થઈ શકે છે; અથવા બંધ લૂપ્સ બનાવી શકે છે જે ન તો કોઈપણ ચાર્જથી શરૂ થાય છે અને ન તો સમાપ્ત થાય છે. ચુંબકીય ક્ષેત્ર રેખાઓ હંમેશા વર્તમાન-વહન વાહકની આસપાસ બંધ લૂપ્સ બનાવે છે કારણ કે ભૌતિકશાસ્ત્રમાં કોઈ ચુંબકીય ચાર્જ નથી. કેટલાક ગાણિતિક સૂત્રોમાં, શક્તિ અને ચુંબકીય સ્ત્રોતોને સંડોવતા ઉકેલો વચ્ચે દ્વૈતતા દર્શાવવા માટે સમકક્ષ ચુંબકીય ચાર્જ અને ચુંબકીય પ્રવાહો રજૂ કરવામાં આવે છે.
બે વાહકો વચ્ચે દોરેલી વિદ્યુત ક્ષેત્ર રેખાઓ ચાર્જનું વિતરણ બતાવવામાં મદદ કરે છે. જો આપણે ધારીએ કે વોલ્ટેજ સ્ત્રોત સાઇનસૉઇડલ છે, તો આપણે અપેક્ષા રાખીએ છીએ કે વાહકો વચ્ચેનું વિદ્યુત ક્ષેત્ર પણ સ્રોતના સમયગાળા જેટલું જ સાઇનસૉઇડલ હશે. વિદ્યુત ક્ષેત્રની મજબૂતાઈનું સંબંધિત પરિમાણ વિદ્યુત ક્ષેત્ર રેખાઓની ઘનતા દ્વારા દર્શાવવામાં આવે છે, અને તીર સંબંધિત દિશા (ધન અથવા નકારાત્મક) દર્શાવે છે. વાહકો વચ્ચે સમય-બદલતા વિદ્યુત અને ચુંબકીય ક્ષેત્રોનું ઉત્પાદન એક ઇલેક્ટ્રોમેગ્નેટિક તરંગ બનાવે છે જે ટ્રાન્સમિશન લાઇન સાથે ફેલાય છે, જેમ કે આકૃતિ 3(a) માં બતાવ્યા પ્રમાણે. ઇલેક્ટ્રોમેગ્નેટિક તરંગ ચાર્જ અને અનુરૂપ પ્રવાહ સાથે એન્ટેનામાં પ્રવેશ કરે છે. જો આપણે આકૃતિ 3(b) માં બતાવ્યા પ્રમાણે, એન્ટેના માળખાના ભાગને દૂર કરીએ, તો વિદ્યુત ક્ષેત્ર રેખાઓના ખુલ્લા છેડા (ડોટેડ રેખાઓ દ્વારા બતાવેલ) ને "જોડીને" મુક્ત-અવકાશ તરંગ બનાવી શકાય છે. મુક્ત-અવકાશ તરંગ પણ સામયિક છે, પરંતુ સ્થિર-તબક્કો બિંદુ P0 પ્રકાશની ગતિએ બહારની તરફ ખસે છે અને અડધા સમયગાળામાં λ/2 (P1 સુધી) નું અંતર કાપે છે. એન્ટેનાની નજીક, સ્થિર-તબક્કો બિંદુ P0 પ્રકાશની ગતિ કરતાં વધુ ઝડપથી આગળ વધે છે અને એન્ટેનાથી દૂરના બિંદુઓ પર પ્રકાશની ગતિની નજીક પહોંચે છે. આકૃતિ 4 t = 0, t/8, t/4, અને 3T/8 પર λ∕2 એન્ટેનાનું ફ્રી-સ્પેસ ઇલેક્ટ્રિક ફિલ્ડ વિતરણ દર્શાવે છે.
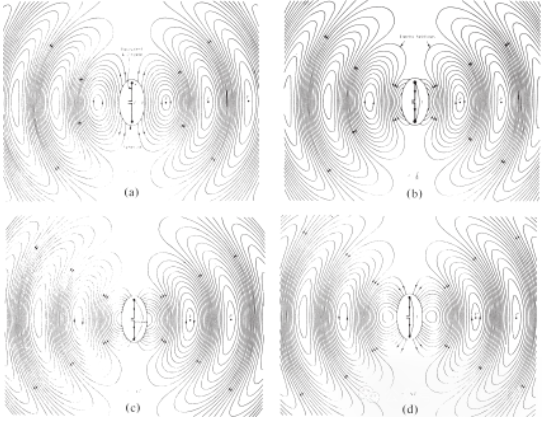
આકૃતિ 4 t = 0, t/8, t/4 અને 3T/8 પર λ∕2 એન્ટેનાનું ફ્રી સ્પેસ ઇલેક્ટ્રિક ફિલ્ડ વિતરણ
માર્ગદર્શિત તરંગો એન્ટેનાથી કેવી રીતે અલગ થાય છે અને આખરે મુક્ત અવકાશમાં પ્રસારિત થાય છે તે જાણી શકાયું નથી. આપણે માર્ગદર્શિત અને મુક્ત અવકાશ તરંગોની તુલના પાણીના તરંગો સાથે કરી શકીએ છીએ, જે પાણીના શાંત શરીરમાં પડેલા પથ્થરને કારણે અથવા અન્ય રીતે થઈ શકે છે. એકવાર પાણીમાં ખલેલ શરૂ થાય છે, પછી પાણીના તરંગો ઉત્પન્ન થાય છે અને બહારની તરફ પ્રસારિત થવાનું શરૂ કરે છે. જો ખલેલ બંધ થઈ જાય તો પણ, તરંગો બંધ થતા નથી પરંતુ આગળ પ્રસારિત થવાનું ચાલુ રાખે છે. જો ખલેલ ચાલુ રહે છે, તો નવા તરંગો સતત ઉત્પન્ન થાય છે, અને આ તરંગોનો પ્રસાર અન્ય તરંગો કરતા પાછળ રહે છે.
વિદ્યુત વિક્ષેપ દ્વારા ઉત્પન્ન થતા ઇલેક્ટ્રોમેગ્નેટિક તરંગો માટે પણ આ જ વાત સાચી છે. જો સ્ત્રોતમાંથી પ્રારંભિક વિદ્યુત વિક્ષેપ ટૂંકા ગાળાનો હોય, તો ઉત્પન્ન થતા ઇલેક્ટ્રોમેગ્નેટિક તરંગો ટ્રાન્સમિશન લાઇનની અંદર ફેલાય છે, પછી એન્ટેનામાં પ્રવેશ કરે છે, અને અંતે મુક્ત અવકાશ તરંગો તરીકે ફેલાય છે, ભલે ઉત્તેજના હવે હાજર ન હોય (જેમ કે પાણીના તરંગો અને તેમણે બનાવેલા વિક્ષેપ). જો વિદ્યુત વિક્ષેપ સતત હોય, તો ઇલેક્ટ્રોમેગ્નેટિક તરંગો સતત અસ્તિત્વમાં રહે છે અને પ્રસાર દરમિયાન તેમની પાછળ નજીકથી અનુસરે છે, જેમ કે આકૃતિ 5 માં બતાવેલ બાયકોનિકલ એન્ટેનામાં બતાવ્યા પ્રમાણે. જ્યારે ઇલેક્ટ્રોમેગ્નેટિક તરંગો ટ્રાન્સમિશન લાઇન અને એન્ટેનાની અંદર હોય છે, ત્યારે તેમનું અસ્તિત્વ વાહકની અંદર ઇલેક્ટ્રિક ચાર્જના અસ્તિત્વ સાથે સંબંધિત છે. જો કે, જ્યારે તરંગો વિકિરણ થાય છે, ત્યારે તેઓ એક બંધ લૂપ બનાવે છે અને તેમના અસ્તિત્વને જાળવવા માટે કોઈ ચાર્જ નથી. આ આપણને આ નિષ્કર્ષ પર લઈ જાય છે કે:
ક્ષેત્રની ઉત્તેજના માટે ચાર્જનું પ્રવેગ અને ઘટાડો જરૂરી છે, પરંતુ ક્ષેત્રની જાળવણી માટે ચાર્જનું પ્રવેગ અને ઘટાડો જરૂરી નથી.
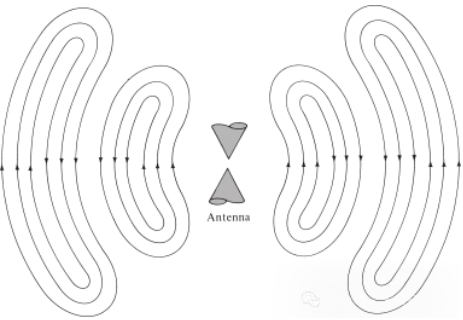
આકૃતિ 5
૩. દ્વિધ્રુવીય કિરણોત્સર્ગ
આપણે એ પદ્ધતિ સમજાવવાનો પ્રયાસ કરીએ છીએ જેના દ્વારા ઇલેક્ટ્રિક ફિલ્ડ લાઇનો એન્ટેનાથી અલગ થઈને ફ્રી-સ્પેસ તરંગો બનાવે છે, અને ઉદાહરણ તરીકે દ્વિધ્રુવીય એન્ટેના લઈએ છીએ. જોકે તે એક સરળ સમજૂતી છે, તે લોકોને ફ્રી-સ્પેસ તરંગોના ઉત્પાદનને સાહજિક રીતે જોવા માટે પણ સક્ષમ બનાવે છે. આકૃતિ 6(a) ચક્રના પ્રથમ ક્વાર્ટરમાં જ્યારે ઇલેક્ટ્રિક ફિલ્ડ લાઇનો λ∕4 દ્વારા બહારની તરફ ખસે છે ત્યારે દ્વિધ્રુવીયના બે હાથ વચ્ચે ઉત્પન્ન થતી ઇલેક્ટ્રિક ફિલ્ડ લાઇનો દર્શાવે છે. આ ઉદાહરણ માટે, ચાલો ધારીએ કે રચાયેલી ઇલેક્ટ્રિક ફિલ્ડ લાઇનોની સંખ્યા 3 છે. ચક્રના આગામી ક્વાર્ટરમાં, મૂળ ત્રણ ઇલેક્ટ્રિક ફિલ્ડ લાઇનો બીજા λ∕4 (પ્રારંભિક બિંદુથી કુલ λ∕2) ને ખસેડે છે, અને વાહક પર ચાર્જ ઘનતા ઘટવાનું શરૂ થાય છે. તે વિરોધી ચાર્જના પરિચય દ્વારા રચાય છે તેવું માનવામાં આવે છે, જે ચક્રના પ્રથમ ભાગના અંતે વાહક પરના ચાર્જને રદ કરે છે. વિરુદ્ધ વિદ્યુતભાર દ્વારા ઉત્પન્ન થતી વિદ્યુત ક્ષેત્ર રેખાઓ 3 છે અને λ∕4 નું અંતર કાપે છે, જે આકૃતિ 6(b) માં ટપકાંવાળી રેખાઓ દ્વારા દર્શાવવામાં આવી છે.
અંતિમ પરિણામ એ છે કે પ્રથમ λ∕4 અંતરમાં ત્રણ નીચેની તરફની વિદ્યુત ક્ષેત્ર રેખાઓ છે અને બીજા λ∕4 અંતરમાં સમાન સંખ્યામાં ઉપર તરફની વિદ્યુત ક્ષેત્ર રેખાઓ છે. એન્ટેના પર કોઈ ચોખ્ખો ચાર્જ ન હોવાથી, વિદ્યુત ક્ષેત્ર રેખાઓને વાહકથી અલગ કરવા અને બંધ લૂપ બનાવવા માટે એકસાથે જોડવા માટે દબાણ કરવું આવશ્યક છે. આ આકૃતિ 6(c) માં બતાવવામાં આવ્યું છે. બીજા ભાગમાં, સમાન ભૌતિક પ્રક્રિયા અનુસરવામાં આવે છે, પરંતુ નોંધ લો કે દિશા વિરુદ્ધ છે. તે પછી, પ્રક્રિયા પુનરાવર્તિત થાય છે અને અનિશ્ચિત સમય માટે ચાલુ રહે છે, જે આકૃતિ 4 ની જેમ વિદ્યુત ક્ષેત્ર વિતરણ બનાવે છે.
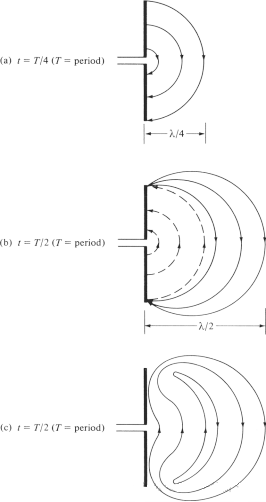
આકૃતિ 6
એન્ટેના વિશે વધુ જાણવા માટે, કૃપા કરીને મુલાકાત લો:
પોસ્ટ સમય: જૂન-20-2024










